「直角三角形の斜辺を、計算によって求める」 第十一回 直角三角形の斜辺を、計算によって求める
単元
直角三角形の斜辺を、計算によって求める
本時の題材
直角三角形の斜辺を、計算によあいさつって求める
メインとなる問題
底辺4cm、高さ3cmの直角三角形の斜辺の長さ
■メイン問題の設定理由■
この単元、最後のクライマックスとなる問題。ずっと面責について学んできたが、それは三平方の定理を具体的な数値で理解することを目的としていた。代表的な整数値の直角三角形、底辺3cm、高さ4cm、斜辺5cmにて、底辺と高さのみ与えられている状態から、斜辺の5cmを導き出す。
これまでの授業で、長方形、平行四辺形、三角形の面積公式を理解し、演習問題にて、辺の長さが直接与えられておらず、まず辺の長さを求めてから面積を導くものについても触れた。また、二つの図形が合わさったものの面積は、それぞれの図形の面積を足したものであることも確認している。それもこれも、三平方の定理につなげるため。これまで学んだことを動員して、三平方の定理に触れる。ここを最終的な目標としていた。
ねらい(この授業で伝えるべき一つのこと)
解説を聞き、全員が「ほんまや!」と、5cmになることを納得する
■"ねらい"の設定理由■
一般的な三平方の定理を証明するためには、文字式を用いる必要がある。が、文字式は学んだことがないので、三平方の定理のもつ普遍性を感じることは難しい。なので、納得することをねらいとし、計算によって辺の長さが求められることを感じてほしい。
どんな直角三角形でも三平方の定理が成り立つという証明では、なかなか三平方の定理を「なるほどー」と納得したり、「ほんまや!」と実感することはおそらく難しい。なので、”ねらい”を「理解」まで結びつけることではなく、斜辺が導き出せることを実感し、その計算や図形の見方に納得することとした。
納得するためには、順序立てて考え、一つ一つを理解し、組み立てていく必要がある。こちらが主体で組み立てていくことになるが、その流れを理解し、論理的に考えることに触れてもらう。
授業の板書と流れ
あいさつ、5分間の計算
メインの問題の提示
今日は、2000年以上前から変わらずにずっと存在する、一つの式について伝えること、今回はぼくがペラペラとたくさんしゃべること、問いかけに答えながらついてきてほしいことを伝える。
三角形の画用紙を用いて、今回のメインの問題「底辺3cm、高さ4cmの直角三角形の、斜辺の長さはいくらか?」を提示する。
あてずっぽうでいいので、何cmになると思うか聞く。「どれになるやろねー」とどれが正解か探りながらついてきてほしいことを伝える。
必要な知識の提示
必要な三つの基本的事柄を確認する。
1、長さについて
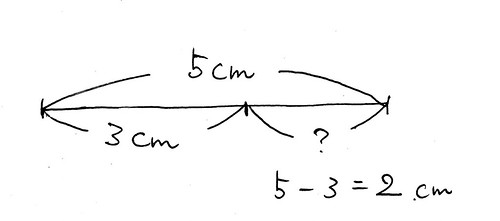
2、面積について
3、正方形の面積と辺の長さについて
面積から辺の長さを求めることができる
この三つと、あとは面積を求めることができれば、今回の?の部分の長さは求められることを強調する。ちなみにこれらはすべて既知の事柄。
メインの問題を解説する
先に提示した直角三角形を用いて、斜辺と等しい長さを辺の長さにもつ正方形を作図する。
正方形の面積がわかれば、辺の長さが求まることを確認し、今から正方形の「面積」を求めていくという方針を理解させる。
正方形に三角形を敷き詰めていく。真ん中にできるのは正方形で、正方形も埋め合わせる。
三角形4つと、小さい正方形一つでぴったり敷き詰められることを提示し、三角形4つと正方形一つの面積を足せば、大きな正方形の面積になることを確認する。
三角形の面積を求める。
小さい正方形の辺の長さを、「必要な知識1」を利用して求める。
小さい正方形の面積を求める。
ここで、はじめからの流れを一度確認する。
大きな正方形の面積を、4つの三角形と小さい正方形の面積を足し合わせて、求める(「必要な知識2」)。25㎠になることを計算する。
「必要な知識3」より、正方形の辺の長さは5cmであることを求める。
大きな正方形の辺の長さと、三角形の求めたい辺の長さが同じであったことを確認し、答えは5cmと求めることができたことを解説する。
解説と同じ流れをなぞる、穴埋めプリントに取り組む
机間巡視し、手が止まっていれば、一つ一つを確認しながら解説する。
使用プリント
20151217_数5G_直角三角形の斜辺を計算で求める.pdf - Dropbox
振り返り
■今回の評価できる点は?■
三角形の求めたい辺で正方形を作図して、そこに三角形を敷き詰めていく、という流れ。
■今回の改善点は?■
解説主体の授業で、みんなの集中が続かなかった。
難しい内容をかみくだいて提示することで、理解を引き出そうという意図だったが、難解に感じる生徒が多く、やる気をそいでしまった。
伝えたいことがあったものの、それを伝わる形で提示することができなかった。
みんなの反応が悪すぎて、ちょっとうろたえ、悪い雰囲気を打開することができなかった。
室温が少し高く、ぽかぽかしていたので、眠気を誘いやすい環境になってしまっていた。
◆今回の「教訓」◆
環境への気配りは大切。
「やる」活動を授業内に含めたほうが、集中を引き出すことができる。解説をメインでしたい授業であっても、どこかで実際に手を動かす活動を入れるべき。
「直角三角形の斜辺を、計算によって求める」 第十回 三角形や長方形を組み合わせた図形の面積
単元
直角三角形の斜辺を、計算によって求める
本時の題材
三角形や長方形を組み合わせた図形の面積
ねらい(この授業で伝えるべき一つのこと)
面積を求めるためには、辺の長さが必要であることを理解する
■"ねらい"の設定理由■
これまでは、問題の中に「タテ」や「ヨコ」、「高さ」など、面積を求めるために必要な辺の長さが提示されている問題ばかりを扱ってきた。が、直角三角形の斜辺を計算によって求める際には、与えられている辺の長さから、求めたい図形の辺の長さを計算し、面積を求めていかなければいけないので、そこにつながるよう、今回のねらいを設定した。
「答えを求めるためには、何が必要か?」考えることは、とても大事な思考の流れであるので、そこを強調し、意識づけるためのねらいでもある。
メインとなる問題
辺の長さを導き、面積を求める問題
■メイン問題の設定理由■
”ねらい”の達成のために、面積を求めるために必要な部分の長さが与えられていない問題をメインに。
そこに至るまでに、まずは辺の長さが与えられている長方形や平行四辺形、三角形の面積を求める基本問題をする。その際に、不必要な部分の長さも与えておき、再度「底辺」や「高さ」という語句の確認をし、図形の中でどの部分の長さが必要かを確認する。その後、メインの問題へ。
授業の板書と流れ
・あいさつ、5分間の計算 [13:30]
あいさつで授業が始まることを意識づける。
計算は集中させる。
・面積の公式、軽い復習 [13:35]
長方形、平行四辺形、三角形の面積の公式を質問し、答えが出た後、それぞれの図と公式を書いた画用紙を黒板に貼ったままにしておく。
・基本問題演習→答え合わせ [13:50]
各辺の長さが与えられている、長方形、平行四辺形、三角形の面積の問題(必要でない部分の長さも与えられている)のプリントを配布し、各自取り組ませる。
机間巡視し、適宜個別に解説。その際、「どの図形か?公式は?どの部分の長さが必要?」かを問うことで、答えへと導いていく。
解くのが早い生徒に対しては、別途1枚プリントを用意しておく。
答え合わせの際、「どの図形か?公式は?どの部分の長さが必要?」を問い、確認させる。
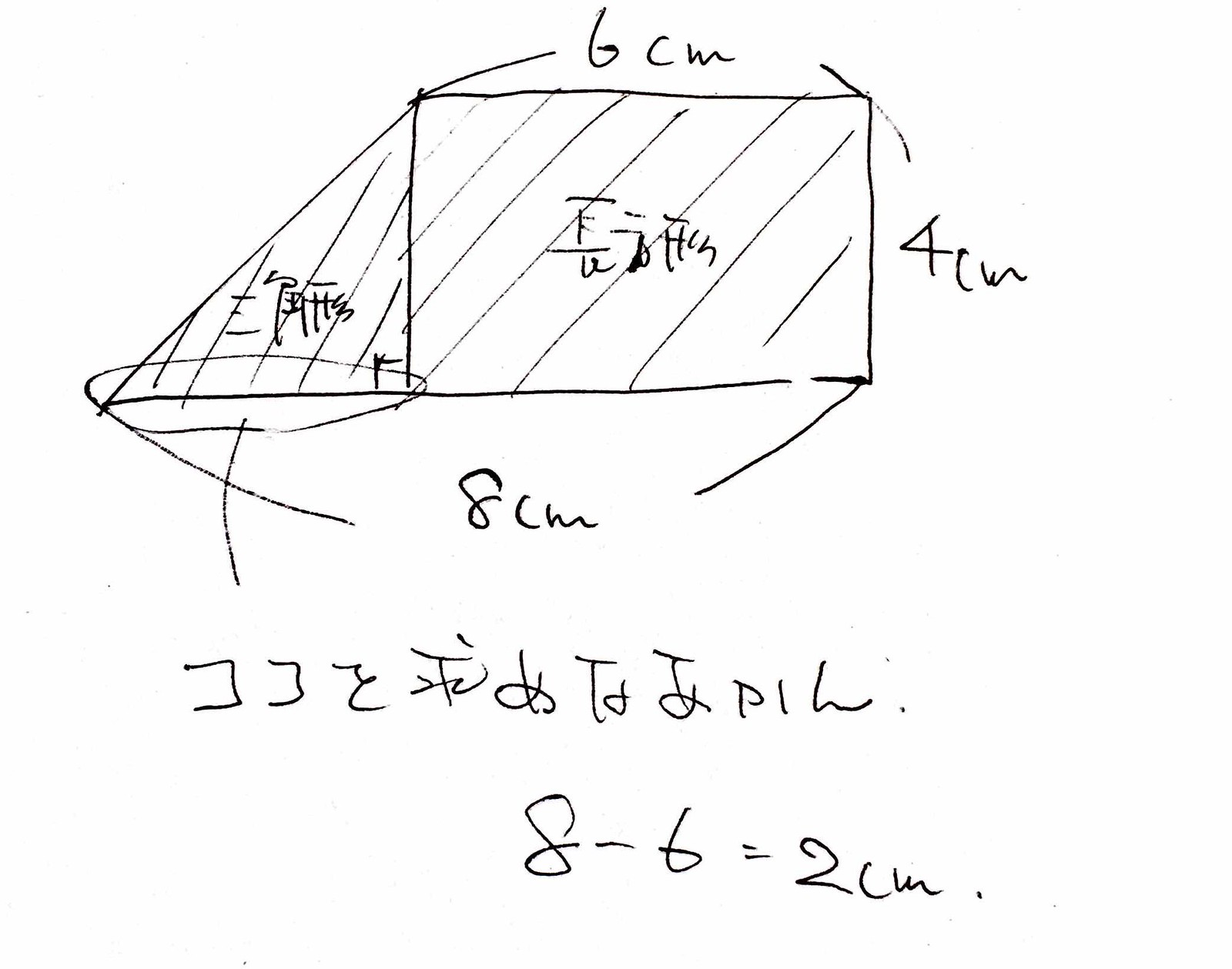
・辺の長さを導き、求める問題 [14:00]
「どうやって求めよう?」「どんな図形がある?」「どこの長さが必要?」
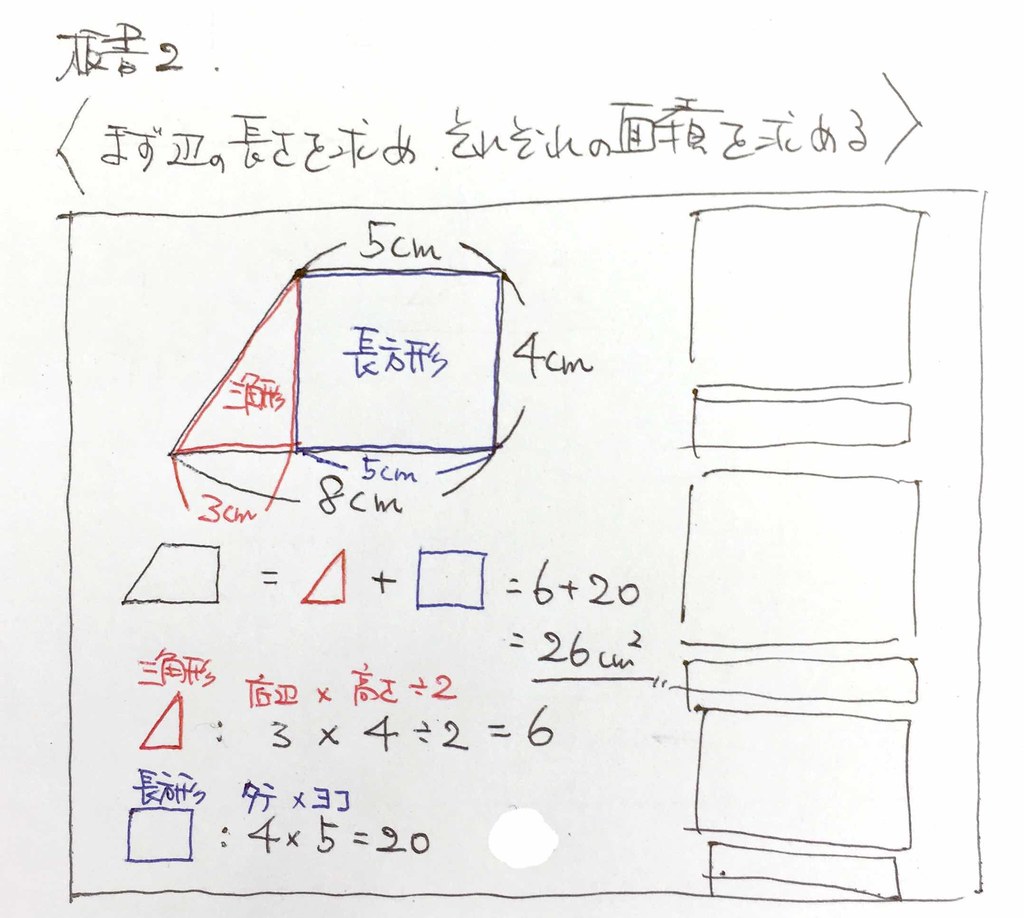
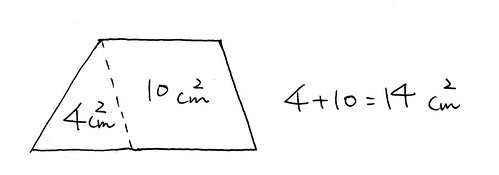
三角形と長方形が合わさった図形であること、それぞれ求めて足し合わせれば全体の面積が出ることを確認。
長方形の面積ではタテとヨコが、三角形の面積では底辺と高さが必要であることを確認し、それらを求める。
それぞれ計算し、足し合わせる。
板書計画
・辺の長さを導き、求める問題演習 [14:17]
辺の長さを導き、面積を求める問題の演習プリントを配布、各自取り組ませる。
机間巡視し、適宜個別に解説。その際、上記三つ「どうやって求めよう?」「どんな図形がある?」「どこの長さが必要?」を問いかけ、意識づけ。
解くのが早い生徒に対しては、さらにいろんな図形の面積の問題を配る。
答え合わせをする。その際、「どんな図形がある?」「どこの長さが必要?」を問い、答えさせ、存在する図形を明確にし、必要な辺を明らかにする。
・まとめ、あいさつ [14:20]
「どんな図形があるのか?その図形の面積を求めるためには、どこの長さが必要か?」に注目していくことが必要であることを振り返る。
振り返り
■今回の評価できる点は?■
演習を多く取り入れてたのはよかったんかも。解ける演習を盛り込んでれば、みんな集中して取り組むことができる。
■今回の改善点は?■
基本の次の問題のチョイスがミスったね。このクラスでは、基本の形の次は、基本の形どうしを組み合わせた問題へ、その次に今日の「辺の長さを導き、面積を求める問題」をもってくるべきやった。一つステップを飛ばしたがために、大半がポカーンとする授業になってしもうた。
◆今回の「教訓」◆
スモールステップで、少しずつ着実に理解させていく進め方のほうが、手が止まる子が少なくていい。既知を未知につなげるような、つながるような、課題設定が大切。
使用プリント
「直角三角形の斜辺を、計算によって求める」 第九回 三角形の面積の演習
単元
直角三角形の斜辺を、計算によって求める
本時の題材
三角形の面積を求める演習
ねらい(この授業で伝えるべき一つのこと)
三角形の面積を理解し、面積を求められるようになる
■"ねらい"の設定理由■
前回の授業での、三角形の面積の解説がいまいちやったという感覚があり、今回の復習で再度「三角形の面積」は「平行四辺形の面積」の半分であることを確認し、理解を促したい。また、直角三角形の斜辺を求める際、直角三角形の面積と正方形の面積を利用する。なので、三角形の面積は自力で求められるように、演習を積み、底辺×高さ÷2を定着させることがねらい。
メインとなる問題
いろいろな三角形の面積を求める問題
■メイン問題の設定理由■
前回は、鋭角三角形についてしか、平行四辺形の半分になっていることを確認していない。他の直角三角形と鈍角三角形についても長方形や平行四辺形の半分になることを確認し、底辺はどこか、高さはどこかを判断できるように、いろいろな三角形について面積の問題を出題する。
授業の板書と流れ
振り返り
■今回の評価できる点は?■
提示の順番を考え、より伝えたい事である「三角形の面積は、平行四辺形の半分である」ってことが見えやすいようにすることができたと思う。同じ三角形をふたつ並べて平行四辺形をつくり、その淵をなぞって平行四辺形を書くことで、三角形はその半分であることを印象付けれた。
■今回の改善点は?■
授業の板書計画と流れの最後のひと練りができなかったこと。じっくり考え、流れは頭の中に入っていたものの、最後にまとめて確認するというプロセスは必要。
■今回の「教訓」■
何を、どのように、どんな順番で提示するのかは、すごく大切。毎回時間をかけて考えていきたい。